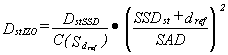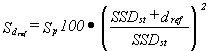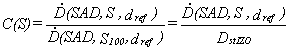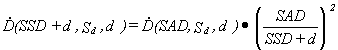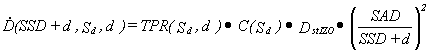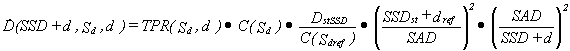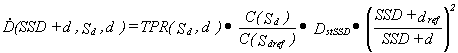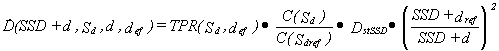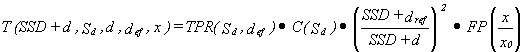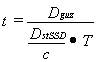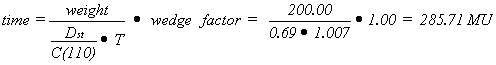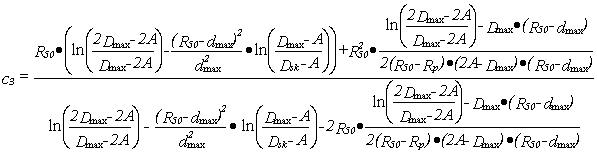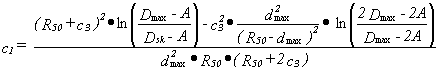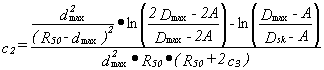The ALFARD tele-radiotherapy
planning system has been created as a result of collective efforts of a team of
specialists - physicists and computer programmers. It took several years to put
the basic version of the System to work. The software to compute and present
the distribution of ionising radiation doses inside the patient=s outline is still under development and new functions are being added.
This part of the documentation (related with System version 8.0)
describes the computational section of the ALFARD
tele-radiotherapy planning system and comprises information regarding:
- measurement and computation techniques,
- dosimetry,
- methods of irradiation and determination of
irradiation time.
Presentation of all
details of the used algorithms is impossible and not necessary. The users of
our planning system will use only the selected information. Sometimes it is
worthwhile to remind some definitions and formulae.
Here you can find a
description of the algorithm applied to obtain distribution of photon doses on the basis of TPR (Tissue-Phantom-Ratio).
The derivation of more important formulae was presented and interrelations
between the basic values used by physicists and radiotherapist were specified.
Chapter 6 describes the method of calculations of the dose for electrons.
Chapter 8 provides an example of preparation of measurement data. The formulae
are given in the form of Pascal programming language routines in order to
specify such factors as TPR(S,g) and C(S).
In this manual you
will not find information concerning programming. In particular no explanation
was given for the algorithm to establish the iso-lines, or other important
geometrical routines, which are reserved for exclusive use of Laboratory of
Computer Systems.
The absorbed dose rate
is measured using an ionisation chamber in a tissue-resembling phantom. The
measurement using an ionisation chamber yields the exposure value (typically in
R/MU or R/min). In order to obtain the absorbed dose rate (in cGy/MU or
cGy/min) the obtained exposure must be re-computed using the necessary factors
in conformance to the recommendations of the used dosimetry protocol.
Below we specify how to measure the output dose rate for a treatment
unit. Conditions, which were assumed as standard in this document, are as
follows:
- for fixed SSD technique, the
measurement is made:
a) at the distance between the
source and phantom surface (SSD) of
100 cm (80 cm);
b) for the irradiation field size
defined on phantom surface and equal: 10x10 cm2;
c) on the depth dref (e.g.
for Co-60 and photons 9 MV - 5 cm);
d) for measurement time tm, (e.g. 200, 300 monitor units [MU]
or 1 minute - depending on the type of unit);
- for the isocentric technique the measurement is made:
a) with source-isocentre (SAD)
distance of 100 cm (80 cm);
b) for the irradiation field size defined in the isocentre and equal to
10x10 cm2;
c) on the depth dref;
d) for time of measurement tm (e.g. 200, 300 monitor units
[MU] or 1 minute - depending on the type of unit).
The depth of the point of reference dref
is determined by recommendations of dosimetry protocols, for each type and
energy of radiation. According to the report no. 277 IAEA the reference depth
for photons is determined by the radiation beam quality defined by the quality
factor 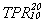 (a ratio between TPR at depth of 20 cm and at depth of 10
cm, for field dimensions 10x10 cm). For radiation beams, for which
(a ratio between TPR at depth of 20 cm and at depth of 10
cm, for field dimensions 10x10 cm). For radiation beams, for which 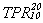 falls below 0.716, it
is recommended to use dref =5
cm. For higher energy dref =
10 cm. In case of electrons the output dose rate is measured at the maximum
dose depth, which means that dref varies for various energies.
falls below 0.716, it
is recommended to use dref =5
cm. For higher energy dref =
10 cm. In case of electrons the output dose rate is measured at the maximum
dose depth, which means that dref varies for various energies.
In this manual the output dose rate measured within the assumed conditions
as above is referred to as " standard dose" - Dst. The standard dose determines the treatment unit
output and is used to calculate the irradiation time and dose in any point of
the irradiated area.
The dose rate in any
point of the irradiated area can be computed using:
- a function expressing decrease of the absorbed dose as a function of
depth along a beam axis (e.g. a percentage depth dose curve);
- function of profile FP(x/x0),
i.e. distribution of absorbed dose along the axis, which is perpendicular to
the axis of the beam of radiation and parallel to one of the sides of the
irradiation field (fig.2);
- standard dose, i.e. the output dose rate measured in standard
conditions;
- a factor expressing relation between dose rate and the size of
irradiation field (e.g. C(S)).
The distribution of doses along the beam axis, as a function of field
size and depth in the absorbing media can be described by means of:
a) the percentage depth
dose PDD (used in computations for
fixed SSD technique);
b) TPR factors (used in isocentric techniques).
The percentage depth dose is given by the formula:
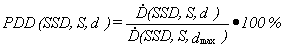 (1)
(1)
where:
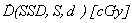 - the dose rate at depth
d [cm] along the beam axis;
- the dose rate at depth
d [cm] along the beam axis;
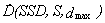 - the dose rate at the depth of maximum dose dmax;
- the dose rate at the depth of maximum dose dmax;
S [cm2] - the irradiation field size on the surface;
SSD [cm] - the distance between the source and the surface.
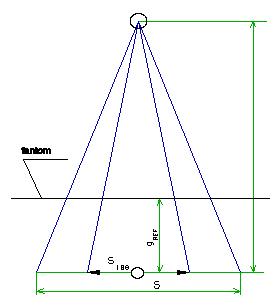
Tissue Phantom Ratio (TPR) for a given field S is defined as the ratio of doses along
the beam axis at depth d and at depth
of reference. The distance between the chamber and the source of radiation and
beam cross-section at that distance are the same in both measurements (fig. 1).
In practice the measured point is selected in the isocentre.
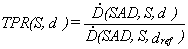 (2)
(2)
where:
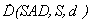 - the dose rate at
depth d, assuming the distance
between the source and measured point equal to SAD;
- the dose rate at
depth d, assuming the distance
between the source and measured point equal to SAD;
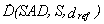 - the dose rate at
depth dref;
- the dose rate at
depth dref;
S - field size (defined in
isocentre);
SAD - Source Axis Distance (distance source - isocentre);
dref - reference depth (5 or 10 cm depending on energy)
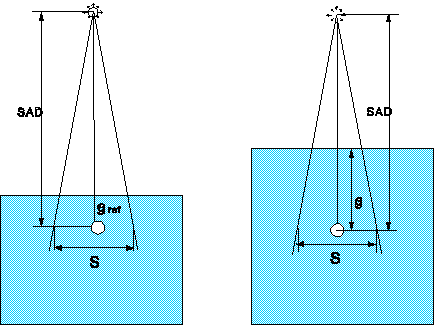
Fig.1
The relation between PDD and TPR is as follows:
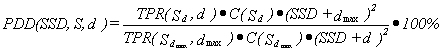 (3)
(3)
where:
S - the irradiation field size on a phantom surface;
Sd - the irradiation field size at depth d (at a distance of SSD+d
from the radiation source);
Sdmax - the irradiation field size at the maximum dose depth.
If the distance between the radiation source and the surface of the
irradiated object is SSD1,
not SSD, PDD must be recalculated for new conditions using the following
formula:
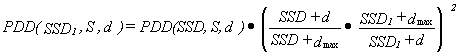 (4)
(4)
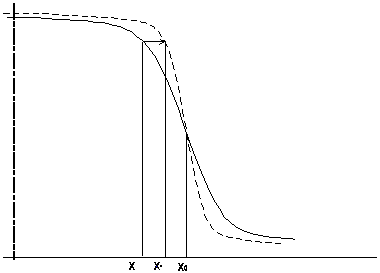
The function of profile (fig. 2) provides the distribution of absorbed dose along an axis perpendicular to
the beam axis and parallel to one of the sides of the radiation field.
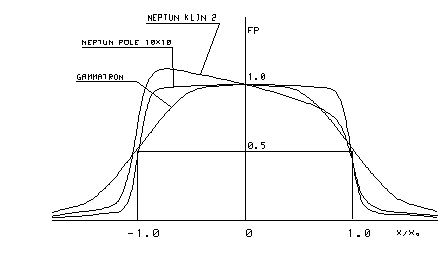
Fig.2
The function of profile depends on the field size, depth and SSD. In
order to compare the functions of profile for various fields and depths,
parameter x0 was
introduced, defined as:
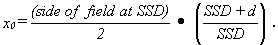 (5)
(5)
Thus, x0 is related
to the field size of the beam at depth d.
If x represents distance from the
beam axis, then for the photon radiation the function of profile FP(x/x0) does not depend (for
a wide range of values) on the depth and field size. The function of profile is
normalised to unity in the beam axis that is FP(0)=1.
The main sense of the profile function for abscissa x/x0 is explained in fig. 3.
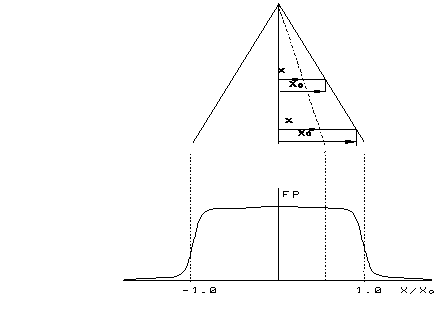
Fig.3
In the case of photon beams the planning system uses in calculations one
or more profiles function FP(x/x0),
irrespective of the depth and applicable for a specific range of irradiation
field sizes. For the electron beams the profile function is modified depending
on depth.
The standard dose represents the dose rate measured in the standard
(reference) conditions described in chapter 2. The standard dose defines the
treatment unit output and establishes the basis in calculations of dose
distribution and irradiation times, made during planning of patient treatment.
The standard dose for isocentric technique has been denoted as:
DstIZO = 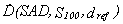
where:
SAD - the distance between the source and the isocentre;
S100 - the field of 10x10 cm2 determined at depth dref and at a distance of SAD;
dref - the point of reference depth.
The standard dose for
the fixed SSD technique has been
denoted as:
DstSSD = 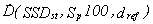
where:
SSDst - standard distance between the source and phantom surface, for which
the standard dose is measured (e.g. 100 cm);
Sp100 - the field of 10x10 cm2 determined on a phantom surface;
dref - the point of reference depth.
Depending on the irradiation technique used, it is necessary to know the
treatment unit output dose rate (the standard dose) either for a given SSD, or in the isocentre. In practice,
one of the standard doses is measured - usually for fixed SSD technique. The standard dose for the isocentric technique can
be determined from the formula:
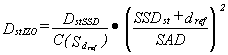 (6)
(6)
where:
C(Sdref ) - the field size factor, described below;
Sdref - the field size at depth dref,
which equals:
The field size factor (fig. 4) is defined on a reference depth dref in the beam axis as a
ratio of dose rate for field S and a
dose rate for a field of 10x10 cm2. The measurement of C(S) must be made in the isocentre,
where the field size is determined.
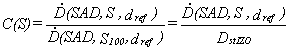 (8)
(8)
Fig.4
The program computes the
distributions of doses for the photon radiation on the basis of the following
data:
·
TPR(S,d) factors
·
field size factors C(S)
·
profile functions FP(x/x0)
·
a patient outline, taking into
account the density of tissues.
For a given point P the
relation between the dose rate and TPR
and C(S) factors can be derived as
shown below.
If the point P is located in
the isocentre and at depth d (cf.
fig. 1), then on the basis of formula (2) we can write for field Sd:
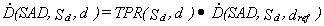 (9)
(9)
Using formula (8) for the field size factor C(S) we obtain the dose rate for any field Sd as:
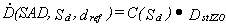 (10)
(10)
Formulae (9) and (10) yield:
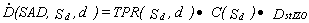 (11)
(11)
If the point P is located on
the beam axis, at a distance SSD+d
from the source, which is different from SAD
(fig. 5), then the dose rate varies with the square of the distance:
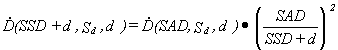 (12)
(12)
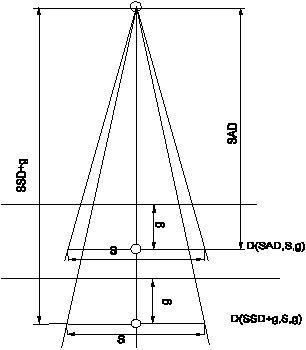
Fig.5
Combining the formulae (11) and (12) we can calculate the dose rate
along the beam axis for any SSD,
field size and depth.
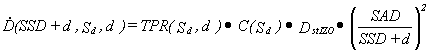 (13)
(13)
In case when we perform a routine measurement of the standard dose using
the fixed SSD technique, the unknown
value of DstIZO in the
formula (13) must be replaced by the measured value DstSSD on the basis of the formula (6).
which finally yields:
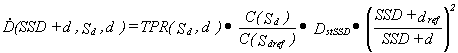 (14)
(14)
If we perform calculations for the media of different density, the TPR factor must take into account the
effective depth def. In
that case the formula (14) can be rewritten as follows:
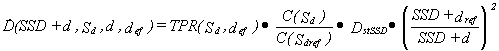 (14a)
(14a)
The dose rate beyond the beam axis, calculated using formula the (13) or
(14), must be corrected by the profile function FP(x/x0) (due to dose variation as a function of
distance from the beam axis):
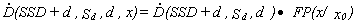 (15)
(15)
Calculation of the dose in a point located within the patient=s outline consists of:
1. calculation of geometrical parameters;
2. determination of effective depth (with taking into account the density);
3. calculation of doses on the basis of geometrical data, functions TPR, C(S) and FP(x/x0).
The geometry of
calculations will be described using an example shown in fig. 6. Point A represents the radiation source, while
sections AB and AC represent the boundaries of the radiation beam (in this way
points B,A,C determine the beam BAC). The curve containing points F and D is a part of the patient=s outline.
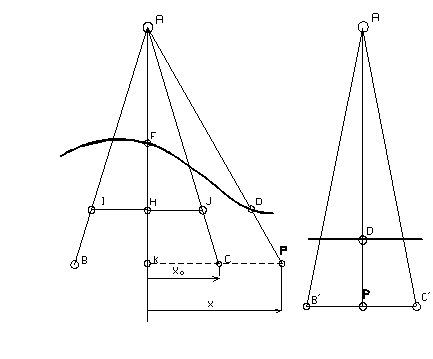
Fig.6
For establishing the
dose in the point P the following
operations are performed:
- find the point where the
section AP crosses the outline, which
gives the point D. Section DP represents the geometrical depth (d) of the point P, measured along the straight line, which connects P with the radiation source and is used
to recalculate the dose rate, in case of distance changes. The depth d and density of the medium enable to
evaluate the effective depth def
used to determine the value of TPR.
- assume the half line AP as an axis of the new beam B'AC' such that the point P, which lies on this axis, at the
distance AP from the source of
radiation, is located at depth DP;
- make an orthogonal projection of point P on the axis of beam BAC;
- determine the value of the
side of beam BAC at a distance AK from the source basing upon the value
of the side defined at the distance AH
from the source.
- with the geometrical depth DP, effective depth and the value of the
side of beam 2KC known, calculate the dose rate in the point P on the axis of B'AC' beam, using the formula (14a);
- find the ratio x/x0 for the point P, that is, determine the quotient of
distances of points C and P from the axis of beam BAC (these are sections KC and KP);
- read out the value of FP(x/x0) for that value of x/x0, which, together with
the previously calculated dose rate
along the beam axis, yields the value of dose rate in the point P.
Assuming in the formula (14a) the factor 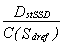 , related to the unit output, being equal:
, related to the unit output, being equal:
to one, we can define the dose
rate factor - T:
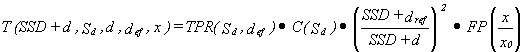 (16)
(16)
The T factor is a
dimension-less value representing the ratio between the dose rate in the point
of calculation and the standard dose.
The factor SSDst+dref relates
to the conditions of measurement of the standard dose. It is a fixed value,
determined by the user.
Note: The numerical values of SSDst+dref
and DstSSD are entered in the main menu of the beam input table,
separately for each unit
The successive steps
of the procedure of calculation the distribution of doses are as follows:
a) a matrix of points lying
within the patient=s outline is generated;
b) density value is assigned
to each point in the matrix:
- if the outline originates from a CT, densities for all points are
calculated using Hounsfield numbers;
- if the outline was input from a digitizer, then the densities are
determined using supplementary contours.
c) the geometrical parameters of all the matrix points are determined
for each beam;
d) the T factor values are calculated in the matrix points, according to
formula (16);
e) the calculated T-values are saved in a two-dimensional array,
separate for each beam;
f) the arrays of results are written into a text file.
The next stage is
presentation of results:
a) the result arrays
for each beam are read from the disk;
b) each of the arrays
of T factors is normalized to the beam weight in the centering point;
c) the arrays obtained
are summed up in order to obtain the distribution of total dose;
d) a maximum value in
the total dose distribution is searched;
e) the following
operations are possible for each matrix:
- changing of dose weight in the point of centering;
- changing of irradiation time;
- modifications or entering of a wedge or tray factor.
- Individual beams can be included or excluded from a summation of
matrices.
f) for a total dose
matrix it is possible to:
- present the dose distribution in the form of isodoses;
- read the dose in any point;
- normalize the distribution to any dose value in any point;
- determine an average dose and compute a histogram for a selected group
of points (area of interest).
4.2.1 Evaluation of effective depth
Calculation of dose, taking into account the medium density, is made
using a method of effective depth. Let us consider fig. 7, which shows section DP (from fig. 6) on the background of a
computation grid, and an area of a different density.

Fig.7
The successive steps
of determination of the effective depth are as follows:
a) the section DP is divided into N sub-sections (points 1..4 marked in fig. 7);
b) the density in each of determined points is computed using a method
of linear interpolation between the closest points. As an example, fig. 7 shows
the point no. 2 on the section DP and
two neighboring points with the densities of d1 and d2.
The density in point 2 depends on the densities d1 and d2
and distances between these points and point 2 (fig. 8). The density in the
point 2 is given as:
The presented example shows a general idea. In practice, interpolation
is made in two dimensions, which means that four nearest points are taken into
consideration.
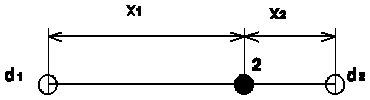
Fig.8
c) since the density
values in the points 1, 2, 3, 4 and P
are known, we determine the average density for the point P;
d) we compute the
effective depth def for
the point P by multiplying the
average density by the geometrical depth d.
4.2.2 Rotational technique
Computation of dose distribution for a rotational beam requires to pull
this beam down into a series of stationary beams distributed uniformly within
the angle of rotation. Each stationary beam is calculated separately, using the
isocentric technique. The distribution of dose is obtained through a summation
of doses coming from stationary beams. The number of these beams depends
on the angle of rotation and the angle
of leap (equal to 5°, 10° or 15°) and can be obtained from the formula:
The time weight for each of the beams defined above is assumed to be 1.
After all the beams are computed and the matrices of T-factors are summed up,
it is time for the presentation of results.
The irradiation time is calculated from the formula:
where:
Dtumor - the planned dose in
the point of tumor;
 - the absorbed dose
rate in the point of tumor.
- the absorbed dose
rate in the point of tumor.
The dose rate can be calculated with the formula presented below which
is obtained from the formulae (14) and (16) and basing upon the standard dose
measurement for SSD
technique.
If the wedge filters are used, the irradiation time is obtained by
multiplying the irradiation time for an open field ((17)) by wedge factor Ww.
t(with wedge) = t(without wedge) H Ww
The wedge factor
tells, to what extent was the dose rate weakened by the wedge. This factor is
defined as a ratio between the dose rate on the beam axis without the wedge
filter, on the depth of reference in the phantom, and the dose rate in the same
point, but with the wedge installed.
The irradiation field
size must be set according to the maximum field for a given wedge.
Application of wedge
filters shifts the position of the maximum dose point beyond the beam axis. In
such a case the determination of the value of the maximum dose requires the
distribution of isodoses to be known.
5.1 Sample printouts with comments
Lines 1 to 7 in the computation report (printout no. 1) are taken from
the table, which we fill in on the screen, and contain the main parameters of
the beams. Line 8 contains the co-ordinates of centering points, beam weights
and the total dose computed in these points. Bear in mind that the total dose
is composed of a dose from the given beam and doses from neighbouring beams.
The beam weights are defined in the main table, but they can be modified on the
stage of adding the beams in the program OBRAZ. Line 9 contains co-ordinates of
the normalization point of the dose distribution, as well as the doses from
individual beams and the total dose in that point. Similar data is given in
line 10, which, however, apply to the maximum dose point. Line no. 11 contains
values of the standard doses DstSSD
for individual treatment unit. Line 12 provides the wedge factors. If no wedge
was applied, then the wedge factor equals 1. The wedge factors for each unit
are stored in the file KLINY.DAT. The depths of centering points are printed in
line 13. Line 14 provides, separately for each beam, the irradiation time
required for the dose in the centering points and determined by the weight.
The final lines in the printout no. 1 provide the location and value of
the maximum dose for a total dose distribution, the co-ordinates of the
normalisation point and the dose value in that point, as well as the number and
values of isodoses on the dose distribution plot.
The dose value in the
normalisation point is closely related to the weights of beams in the centering
points. For instance, if we increase the dose in the normalisation point by
e.g. 23%, then the weight value for each beam will also rise by 23%. This can
be done while defining the normalisation point in the program OBRAZ.
Printout No. 1
.-------------------------.
/
Laboratorium Systemów \
| Komputerowych Gliwice |
\
SYSTEM ALFARD V8.0 /
`--------------------------'
Computation date: 1994.4.15 (Friday), time:
17:24:18
------------------------------------------------
1: | beam no.
| 1 |
6 |
|--------------|----------------|---------------|
2: | technique
| fixed SSD |
fixed SSD |
|--------------|----------------|---------------|
3: | Unit
| SATURN X
| B1 tr 45 |
|--------------|----------------|---------------|
4: |
wedge/block | |
|
|--------------|----------------|---------------|
5: | distance
| ssd100.0cm | ssd 80.0cm
|
|--------------|----------------|---------------|
6: | Initial
angle| 63° | 312° |
| End angle | 63° | 312° |
|--------------|----------------|---------------|
7: | field
size | on skin | on skin
|
|
[cmxcm] | 10.0x10.0 | 9.0x10.0 |
|--------------|----------------|---------------|
|
PC X,Y | 15.0
10.0 | 15.0
10.0 |
8: | Dose
(weight)| 100.0 cGy |
100.0 cGy |
| Σ in PC | 200.0 cGy | 200.0 cGy |
|--------------|----------------|---------------|
9: | PN 6.45,14.4
| 142.3 + 4.117 |
| Σ 146.5 | | |
|--------------|----------------|---------------|
10:|
Max15.0,15.0 | 110.9 +
132.0 |
| Max :242.9 | | |
|--------------|----------------|---------------|
11:| Output
DR |
0.783cGy/JM | 97.87cGy/min |
|--------------|----------------|---------------|
12:|
wedge/tray | 1.00 | 1.00
|
|--------------|----------------|---------------|
13:| depth PC
cm | 13.1 | 11.8
|
|--------------|----------------|---------------|
14:| Irrad.
time | 145.32 JM | 1.6237 min
|
------------------------------------------------
Max. dose point co-ordinates: X=15.0cm
Y=15.0cm, Max. dose value: 242.9
In the normalisation point: X= 6.4cm
Y=14.4cm dose value: 146.5
No. of isodoses: 12
Values: 20.0 40.0 60.0 80.0
100 120 140
160 180 200
220 240
With ref. to P.N.: 13.7 27.3 41.0 54.6 68.3 81.9 95.6 109 123 137150 164
[%]
The value of the dose
power factor T enables the calculation of treatment time for each beam. Given
the value of T in the point of tumor, application of the formulae (17) and (19)
allows to compute the irradiation time required to obtain the dose Dtumor
for the stationary and rotational beams:
where:
t - the irradiation
time [min] or [MU];
Dtumor - preset tumor dose [cGy];
DstSSD - standard dose for fixed SSD
technique [cGy/min] or [cGy/MU];
T - dose rate factor in the centering point (PC), computed and printed by the planning system
c - value of C(Sdref)
which is constant for a given unit.
The main menu of the program provides an the option for calculation of
irradiation time. Select it in order to
check the T factor value and the irradiation time computed by the main program
LICZP.EXE. This option starts the program CZAS.EXE, which produces the printout
no. 2. That printout gives: dimensions of sides of fields on the skin - lines
no. 4 & 5, and sides of fields at depth given in line no. 3, in lines no. 6
& 7. Line no. 8 provides the value of equivalent square field on the skin.
The standard dose for SSD technique can be found in line no. 9. Line no. 10
comprises T factor calculated independently on that printed in the report
(printout no 1, line no. 10). The information is repeated in order to reduce
the chance for a mismatch in computation of the irradiation time.
PRINTOUT No. 2
The control printout for calculation of
treatment time (from the program CZAS):
date 1990.5.15
* * * * * * * * * * * * * * * * *
1 Unit : Neptun
2 SSD : 100.0 cm
3 depth PC : 5.0 cm
4 side A of field on the skin : 10.0 cm
5 side B of field on the skin: 10.0 cm
6 side A of field in PC : 10.5 cm
7 side B of field in PC : 10.5 cm
8 equivalent field size on the skin
: 100.0 cmXcm
9 standard dose : 0.70 [cGy/JM]
10 T
factor : 1.007381
11 wedge factor : 1.00
12 preset tumor dose (weight) : 200.0 cGy
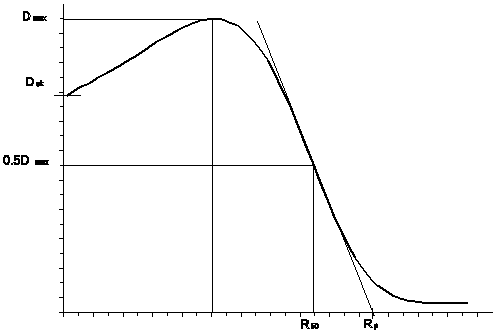
The drop of dose value with depth for electron beam was described by a
function. This function allows to calculate the dose on a given depth on the
basis of known basic physical parameters characterizing the beam of electrons
of a given energy.
In this formula d represents
the depth in millimetres and dmax
- the depth of maximum dose. Factors: A,B,c1,c2,c3
are determined from the maximum dose value, dose on skin, range R50 and practical range Rp.
The A factor is related to the
value of dose generated by bremsstrahlung. In practice, we can assume A as equal to the value of dose at depth
exceeding the practical range of electrons by 3-4 cm.
f(dmax)= A + B = Dmax, then:
B = Dmax - A.
Consequently, the factors c1
and c2 can be established
from the formulae:
f(R50)= 0.5A(A+B).
The skin dose Dsk
(defined as the dose value at depth of 0.5 mm [ICRU Report 35]) may serve as
an approximated value of f(0). Better
results are yielded however by linear extrapolation of the measured data and
determination of dose at the depth of d = 0.
Finally, we shall determine the c3
factor. The value of this factor can be calculated using a relation between the
derivative of f(d) in point d = R50 and a practical range Rp. If we draw the straight line comprising points with
the co-ordinates (R50 ,0.5ADmax) and (Rp,0)
then the slope coefficient of this line gives a good approximation of
the function derivative in point d=R50.
To simplify calculations it was assumed that the practical range of electrons
is determined by the cross-point of the line tangent to the depth dose curve
and the zero dose value level.
Thus by determination of electron beam parameters and using the above
relations we can calculate the factor values for a function expressing the dose
drop with depth. Obviously, in order to give a full characteristic of
therapeutical electron beams we must also take into account the dependence of dmax, R50, Rp,
Dsk on the field size. This is an individual feature of a given
unit.
For the needs of a planning system, the dependence of the parameters
mentioned above on the value of field side was described with reference to
their values for a side of 10 cm. It makes the modification of the depth-dose
function easier - it requires only to update the values of gmax, R50, Rp, Dsk and A factor for field of 10cm x 10cm.
The procedure of computing the doses for electrons uses the profile
functions measured at the depth of maximum dose. To compute the dose for a
different depth a modification is made which changes the profile penumbra. For
the depth values less than dmax
the penumbra is reduced, and for the greater values it increases. This can be
achieved using a simple geometrical transformation, shown in fig. 9.
Fig.9
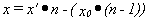
where n is the real number of
the penumbra correction.
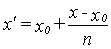
In case when:
n= 1 the penumbra remains
unchanged;
n < 1 the penumbra
shrinks;
n > 1 the penumbra
grows.
Practical calculations showed that n should fall within a range of 0.5 -
2.0. The n value for a given depth g is calculated from the formula:
The formula Ain the box@ is responsible for characteristic appearance of isodoses for electrons.
One of the methods of visualization of dose distribution in modern
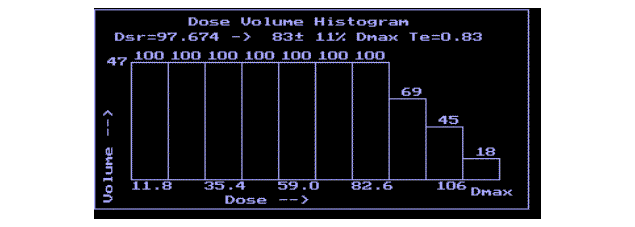
radiotherapy planning system is the Dose - Volume Histogram (DVH). It offers an
easy way to evaluate the uniformity of the dose within the tumor volume and
allows for simply comparison of different plans of treatment.
The axes of this plot represent: absolute dose values (or dose values
with reference to the maximum dose) and a percent of the area which accumulated
the given dose. Moreover, the surface of the area of interest is also given.
The plot provides the information about the average dose in the area of
interest and a standard deviation from the average value.
Another computed parameter, Te,
determines the degree of uniformity of a dose within the tumor volume. Te is defined by a ratio
between two areas in the plot: the total area of all the bars in the histogram
and the area of a rectangle which sides correspond to 100% values of volume and dose. In case, when the tumor area is
selected as the area of interest, this rectangle corresponds to ideal, uniform
distribution of dose with the average value of
100% of the planned dose. Good plans give in the tumor area the
histograms with Te factor close to
unity (0.95 - 0.99). Usually this can be satisfactory. In such a situation the
quality of a treatment plan is determined by evaluation of the histogram in the
critical area. The histogram bars for the critical area should be as low as
possible, and Te should be
close to zero.
Another crucial question is the selection of areas of interest. The
areas should be entered simultaneously with the patient=s outline, before the beams are defined.
The comparison of two plans of treatment should be performed for the
same area of interest.
Below we present an example of processed results of measurements made in
the oncological centre in Bydgoszcz (Poland).
All the measurements
were made using an automatic water phantom which enables measurement of relative dose (two measurement probes) or an
absolute dose (one probe) value.
For each of the unit
the following values were obtained:
1) a percentage depth dose
for a given SSD and for various
fields (defined on the surface of the phantom);
2) profiles on several
depths, for various field sizes;
3) PDD and profiles for various wedge filters;
4) wedge factors;
5) field size factors C(S).
Processing of the measurement data includes:
- calculation of TPR(S,d)
factors basing upon PDD and
describing them by means of an analytical function of depth and the field size;
- "smoothing" the profiles (using Fourier analysis) and a
summation of normalised profile functions (see chapter 3.2) for the given field
size;
- selecting a function describing measured C(S) values.
The functions for TPR(S,d) and
C(S) are presented below, while the
set of profile functions is available from the programs SPLFUN and ROZPAKUJ.
All coefficients occurring in the functions TPR and C(S) were
obtained using the method of least squares.
8.1 TPR function for Theratron 780 C
Processing of results for Theratron 780 C Bydgoszcz
{-----
THERATRON-780 C Bydgoszcz ---}
{ S - field size at the depth g[cm2] }
{ g - depth [cm] }
{ the function approximation for TPR }
{---------------------------------------}
function TPRB(S,g: double): double;
function ww(a,b,c: double): double;
begin
ww := a + b /( c + S );
end;{ ww }
var
C,D,w1,w2,w3,w4 : double;
begin
w1:=ww(
-5.611837E-5, -10.036, 75.2647 );
w2:=ww(
7.654175E-3, -8.6195, 138.971 );
w3:=
0.52121 + 1549.40777/sqr(4.6062 + S);
w4:=ww(
0.039535, 4.9362969, 187.69387);
D:= (1.0
+ 1.0/(2.75 + w3*5.0))*exp(5.0*w4);
if g< 2.0 then
begin
C:= (-1.0/(2.75+w3*2.0))+D*exp(-2.0*w4)-exp(w1*ln(2.0))-(w2/2.0);
TPRB:=
C + exp(w1*ln(g)) + w2/g;
end
else
TPRB:= -1.0/(2.75 + w3*g) + D*exp(-w4*g);
end; { TPRB }
8.2 C(S) factor for Theratron 780 C
The field size factor C(S) was described using a theoretical
formula:
where S represents field size [cm2]
at the depth of 5 cm.
The measurements are
made for SSD=75 cm and g=5 cm (i.e. at isocentre).
A = 0.9381282,
W1 = -1.26650345E+4,
W2 = 261.502686,
W3 = 0.0344054,
s-> 6.419E-03 r->0.9998.
(s - the total of squares of
deviations, r -correlation factor)
8.3 TPR function for Neptun
{------- NEPTUN - Bydgoszcz ------}
{ S - field at the depth
g }
{ g - depth [cm] }
{ the function approximating
TPR }
{----------------------------------}
function TPRByd(S,g:
double): double;
function ww(a,b,c: double):
double;
begin
ww := a + b /sqr( c + S );
end;{ ww }
var
C,w1,w2,w3: double;
begin
if g<=5.0 then
begin
w1:=ww( 23.939538095, -2.902532322E+6, 452.697648263 );
w2:=ww( 0.148189975 , 6.5809876375E+5 , 1.1003592892E+3 );
w3:=ww( 2.319254494 , -1.617226705E+6 , 1.4664107171E+3 );
C:=(1 + w2*exp(-5.0*w3))*sqrt(w1+5.0);
TPRByd:= C/sqrt(g+w1) - w2*exp(-w3*g);
end
else
begin
w1:=ww( 1.70460311 , -1.3295174E+5, 475.409021 );
w2:=ww( 0.015404323786, 1.4150353233E+3, 209.72562283);
C:= 1-w1*exp(-5.0*w2);
TPRByd:= w1*exp(-w2*g)+C;
end;
end; {TprByd}
8.4 C(S) factor for Neptun
The field size factor C(S) was described using an empirical
formula:
where S represents the field size [cm2]
at the depth of 5 cm.
The measurements were
made for SSD=95 cm and g=5 cm.
A = 0.30818289,
w1 = 9.6552494E+3,
w2 = 230.176627,
w3 = 0.13071169.
s-> 1.0432E-02 r->0.9996.
Supplement
In the isocentric technique the tumor (point of centering) is always
located in the isocentre. The distance from the radiation source to the surface
(skin) equals to the difference between the distance source - centering point
and depth of the centering point. The
irradiation field is determined at the isocentre, which is at the depth of the
tumor. This technique is used in rotational therapy, where the distance to the
centering point is fixed, while the distance to the skin changes with the
movement of the source. TPR, C(S) and
DstIZO are related to this
technique. The dose rate in a given point can be computed from the formula
(13).
In the SSD technique the
distance from source to the surface (skin) is constant. The distance between
the tumor (centering point) and the source can be obtained as a sum of the
distance to the skin and depth of the tumor. The irradiation field is defined
at the surface (on the skin).
The following values
are related to this technique: PDG, q(S),
K(S) and DstSSD. The
dose rate in a selected point on the beam axis can be calculated using PDG(SSD,S,d):
where K(S) is a factor representing the
relation between the dose in a maximum and the field size.
Bolus
This is a
tissue-resembling material placed around the irradiated area in order to cause
additional absorption and scatter of radiation. It is also used to compensate
for the oblique direction of the beam entering the irradiated area.
Build-up
This is a phenomenon,
in which the dose grows with depth in material irradiated by an X or gamma
rays. The dose reaches its maximum value on a particular depth, which depends
on the energy of photons. For example the maximum dose depth is about 3 cm for
photons of 23 MV, 2 cm for 10 MV and 0.5 cm for Co-60 gamma rays.
A skin dose
This is a dose
supplied by the radiation beam in a point of interest on the irradiated body
surface. In case of a multi-field therapy the skin dose value may grow due to
the exit dose from other beams.
Standard dose Dst
This is a dose rate
value measured in standard (reference) conditions. It is the base in
calculations of dose distribution and irradiation times when planning the
patient=s treatment.
Phantom
This is a
tissue-resembling material of the volume large enough to ensure full scatter
conditions. Sometimes an anatomical phantom is used, with shape resembling the
patient=s body.
Peak absorbed dose
This is the depth, on
the axis of symmetry of the radiation beam, where the dose reaches its maximum
value (cf. Build-up).
Note: Remember that in
case of application of the wedge filters the maximum dose position can be moved
away from the beam axis and towards smaller depths. This value is not equivalent
to that defined in the heading.
Isocentre
The majority of
therapeutical instruments are designed in such a manner that the radiation
source (focus) can move along an arc around the horizontal axis. The axis of
the radiation beam, which is also a collimator axis, moves in a vertical plane.
The isocentre lies in the cross-point of the rotation axis and the beam axis.
Isodose
This is a line of the
constant dose (usually on a plane).
The tissue-resembling material
This is material, in
which the absorption and scattering of X and gamma rays as well as of electrons
are the same as in a corresponding biological material (soft tissue, muscle,
bones or fat tissue). The best equivalent of the soft tissue is water.
Axis of rotation
This is a straight
line, around which the head of a therapeutical instrument may rotate. The
direction of a rotation axis is horizontal (cf. isocentre).
Beam axis
This is a straight
line, going from the centre of the radiation source to the centre of symmetry
of a figure (rectangle) formed by edges of a diaphragm, which defines the beam
of radiation.
Field
This is the
cross-section of a beam which is perpendicular to the beam axis. The field is
two-dimensional, while the beam is three-dimensional. The field can be defined
at any distance from the source. Furthermore, a distinction is made between:
a. Geometrical field
Geometrical field is shaped by the collimator and is defined as a
projection upon a plane perpendicular to the beam axis. The geometrical field
value can be defined at any distance from the source. In practice the field
value is defined at a distance equal to SSD
or isocentre. Usually the geometrical field is indicated by field simulated
with an optical system using a beam of light.
b. Physical field
It is used in dosimetry. It is defined as the field located between the
isodose 50% on the depth of maximum dose or in the isocentre. In that case the
physical field is greater than the geometrical field. Sometimes the physical
field is defined by isodose 80% or 90%. In that case the physical field is
smaller than the geometrical field.
Percentage Depth Dose %DD(S,d)
This is a percentage
ratio between the dose rate along the beam axis, in a point located at depth d, and the dose rate in the maximum dose
point.
X radiation (bremsstrahlung)
This electromagnetic
radiation is produced when electrons with high energy Abrake@, especially in materials with high
atomic number. The X radiation is generated in X-ray tubes (energy up to
several hundreds of keV) or in linear electron accelerators (energy up to
several tens of MeV ). Its characteristic features are: continuous energy
spectrum and high penetrative properties. It is absorbed by media which it
passes through. The absorption can be expressed by an exponent formula. The
radiation of this type causes ionisation of the media indirectly through
generation of electrons (photoelectric absorption, Compton scattering, or a
positron - electron pair creation).
Point of reference
This is an arbitrary
point located inside the phantom lying on the axis of a beam. The depth of this
point depends on the type and energy of radiation. It can be an isocentre point
or a point of maximum dose rate.
SAD (Source-Axis-Distance)
This is a distance
(along the beam axis) between the radiation source and the rotation axis. This
term is used in the rotational technique.
SSD (Source-Surface-Distance)
This is a distance
(along the beam axis) between the radiation source and the irradiated surface
(skin). This term is used in the technique of stationary beams.
TAR(S,d) (Tissue-Air-Ratio)
This is a quotient of
dose rate values measured along the beam axis in the phantom, at a given depth d, and those measured in the air, in the
conditions of electrons equilibrium. The distance from the source and the beam
cross-sectional area at that distance are identical in both measurements of
dose.
Arc Therapy or Pendulum Therapy
This is an irradiation
technique, in which the beam of radiation moves. The radiation source moves
along an arc around the patient located on the axis of rotation. The distance
between the source and the axis of rotation is constant.
Technique of fixed beams
The tumor area (Target
Volume) is irradiated during different periods of time with one or several beams
inclined at a given angle to the patient. In practice, two techniques of fixed
beams are used: SSD technique and isocentric technique.
TPR(S,d) (Tissue-Phantom-Ratio)
This is a quotient of
dose values measured in the phantom, along the beam axis at a given depth d and at the depth of reference. The
distance from the source and beam cross-sectional area at that distance are
identical in both dose measurements. In practice, the given point of
measurement is located in the isocentre (cf. point of reference). TPR depends
on field size S and depth d.
Field size factor C(S)
The field size factor C(S) is defined as a ratio of dose rate
measured at standard (reference) depth, for the field determined at that depth,
to the value of dose rate for field S=
10x10 cm2.
Note:
The field S= 10x10 cm2, SAD and the depth assume the same
values as for measurement of a standard dose using the isocentric technique.
Field size factor q(S)
q(S) is defined as a ratio
of dose rate measured for field S,
determined on the phantom surface, and the dose rate for field S = 10x10 cm2 with fixed
distance SSD and fixed (reference)
depth of measurement.
Note:
The field S= 10x10 cm2, SSD and the depth assume the same values
as for the standard dose measurement in a
SSD technique.
The wedge factor
This factor is defined
as a ratio of dose measured in a given point located upon the axis of the beam
without the wedge filter, to the dose in the same point with the wedge filter
installed.
Output of a therapeutic unit
This term denotes the
measured dose rate of the radiation
produced by a given treatment unit in precisely defined conditions (cf.
standard dose).
Practical range Rp
Practical range can be
determined from the depth dose curve for electron beam. It is a depth of a point
where the line tangent to the depth dose curve crosses with the straight line,
which determines the level of a dose from the braking radiation (sometimes it
is given as the depth of a point, where the tangent line crosses with the zero
dose level).
Range R50
The range R50
represents such a distance within the phantom, for which the percentage depth
dose falls to 50%.
![]() (a ratio between TPR at depth of 20 cm and at depth of 10
cm, for field dimensions 10x10 cm). For radiation beams, for which
(a ratio between TPR at depth of 20 cm and at depth of 10
cm, for field dimensions 10x10 cm). For radiation beams, for which ![]() falls below 0.716, it
is recommended to use dref =5
cm. For higher energy dref =
10 cm. In case of electrons the output dose rate is measured at the maximum
dose depth, which means that dref varies for various energies.
falls below 0.716, it
is recommended to use dref =5
cm. For higher energy dref =
10 cm. In case of electrons the output dose rate is measured at the maximum
dose depth, which means that dref varies for various energies. ![]() (1)
(1)![]() - the dose rate at depth
d [cm] along the beam axis;
- the dose rate at depth
d [cm] along the beam axis; ![]() - the dose rate at the depth of maximum dose dmax;
- the dose rate at the depth of maximum dose dmax; ![]() (2)
(2)![]() - the dose rate at
depth d, assuming the distance
between the source and measured point equal to SAD;
- the dose rate at
depth d, assuming the distance
between the source and measured point equal to SAD;![]() - the dose rate at
depth dref;
- the dose rate at
depth dref; 
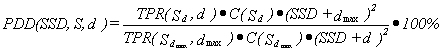 (3)
(3)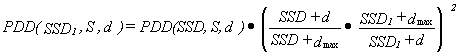 (4)
(4)
![]() (5)
(5)