Wersja 2008-09-14

Opis pliku z dawkami 3D jaki tworzy Alfard dla potrzeb prezentacji 3D

Typ:Plik binarny

liczba short    wersja pliku

3*float            ox,oy,oz //punkt origin

3*unsigned short vx,vy,vz //rozmiar volumenu w pikselach (vx,vy) wymiar tablic, vz ilosc warstw

3*float  sx,sy,sz sx,sy,sz rozmiar siatki (voksela) jest on staly

dalej dane do konca pliku (short)

Dalsza część opisu dotyczy pierwszej wersji tekstowej. Różnica jest taka, że teraz w wersji binarnej występuje jeden nagłówek a dalej idą tylko tablice x/y dawek dla poszczególnych warstw.

Opis jest na przykładzie konturu prostokąta o wymiarach 20x10 cm. Siatka jest bardzo duża i wynosi 2cm co w zapisie jest liczbą 200 bo w mm*10. Program wyznaczył punkty obliczeniowe wewnątrz tego prostokąta. Punkty oznaczone gwiazdkami na rysunku są w odstępach co 2cm. Dawki obliczane w tych punktach są w tablicy dwuwymiarowej. Element (1,1) tablicy ma dawkę 12 i jest dolną lewą gwiazdką o współrzędnych w mm 2,2.

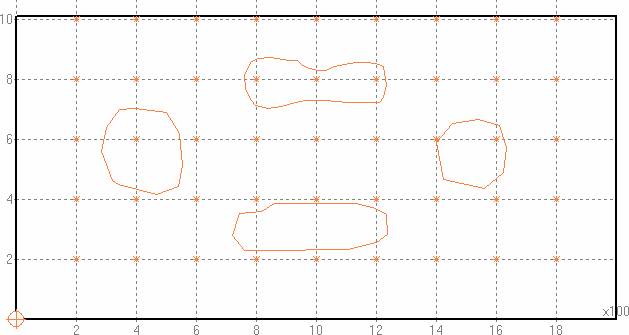
Rys. 1

Zapis dawek dla tego przypadku wygląda następująco:

0 0 0 9 5 200 // x,y,z,ileKolumn,ileWierszy,siatka [mm*10]

12      10      10       9       9       9       9       9       8

      12      11      11      10      10      10      10      10      12

      12      12      12      11      11      11      11      12     100

      12      12      12      12      11      11      12      46     121

   -9999   -9999   -9999   -9999   -9999   -9999   -9999   -9999   -9999

Każdy blok danych zawiera współrzędne dolnego lewego punktu prostokąta obejmującego nawet największy skan są to współrzędne względem offsetu w [mm*10] i np. 3cm jest zapisane jako 30*10=300. Kolejne dane to ilość kolumn i ilość wierszy tabeli, która jest stała dla każdego bloku danych Odpowiedniość punktów na płaszczyźnie i w tabeli prezentują Rys. 2 i zielony fragment pliku Daki3d

Na czerwono zaznaczone są dawki 12 i 121 dla punktów dających się łatwo zlokalizować na płaszczyźnie skanu.

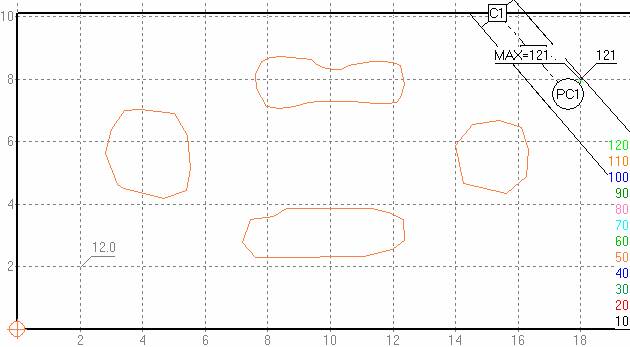
Rys. 2

Płaszczyzny są prostopadłe do osi Z więc współrzędne Z są stałe dla wszystkich punktów związanych z daną warstwą. Siatka czyli odległość między punktami obliczeniowymi w tej wersji jest stała i poziomo i pionowo. Współrzędne x1,y1 dolnego lewego rogu prostokąta obejmującego są stałe. Na Rys. 3 jest przedstawiony rzeczywisty obraz konturu głowy.

Rys. 3

Zakładając położenie płaszczyzny z=-975 dla tego przypadku nagłówek jest następujący

-593 1303 -975 6 8 200 // x,y,z,ileKolumn,ileWierszy,siatka [mm*10]

      10      10       9       6       9   -9999

      10      10      16      12      10   -9999

      10      17      18      18      10   -9999

      11      17      18      18      16       4

       8      16      17      17       9   -9999

       5       8      15       9       7   -9999

   -9999       4       2       7   -9999   -9999

   -9999   -9999       0   -9999   -9999   -9999

Liczby -9999 uzupełniają brakujące nieobliczalne punkty.

Związek między indeksami: kolumna, wiersz a współrzędnymi x i y jest następujący:

· x:=DolnyLewyX+(k*siatka)

· y:=DolnyLewyY+(w*siatka)

Dawka obliczona w danym punkcie może dotyczyć całej kostki o krawędzi równej siatka ale ten sześcian ma środek w punkcie obliczeniowym. Alfard generuje taki jeden sześcian dla punktu dawki maksymalnej. Jest nazywany DawkaMax i umieszczony w zbiorze Siatka3d jako dwa kwadraciki w kolorze czerwonym.